プロフィール
AtCoder PR

AtCoder ABC065B「Trained?」をTypeScriptで解く：ボタン遷移の最短手数（周期検出の入門）

 
AtCoder ABC1065B解説
記事内に商品プロモーションを含む場合があります
Contents
  1. 対象読者
  2. 問題概要
  3. 解き方の全体像
  4. ポイント
  5. 実装例（最小・速い・わかりやすい）
  6. 実装例（堅牢版：訪問済みで早期終了）
  7. サンプルで手計算
  8. よくある間違い
  9. 発展的な実装例（学習用）
  10. 計算量とメモリ
  11. まとめ

対象読者

  • AtCoder初級〜中級
  • 「ABC065Bを最短手数で解きたい」「1-based/0-basedの取り扱いでよく迷う」人

問題概要

問題文（要約＋原文）
AtCoder社の設備には N 個のボタン があり、常に 1 個だけ 光っています。番号は 1..N。
ボタン i が光っているときに押すと、i は消灯し a_i が点灯します（i = a_i の場合も可）。最初は 1 が点灯。
高橋君は 2 が光っている状態 でやめたい。

可能か判定し、可能なら 最小の押下回数 を求めよ。
不可能なら -1。
制約：2 ≤ N ≤ 1e5、1 ≤ a_i ≤ N
入力：

N
a1
a2
...
aN

出力：最小回数 or -1

解き方の全体像

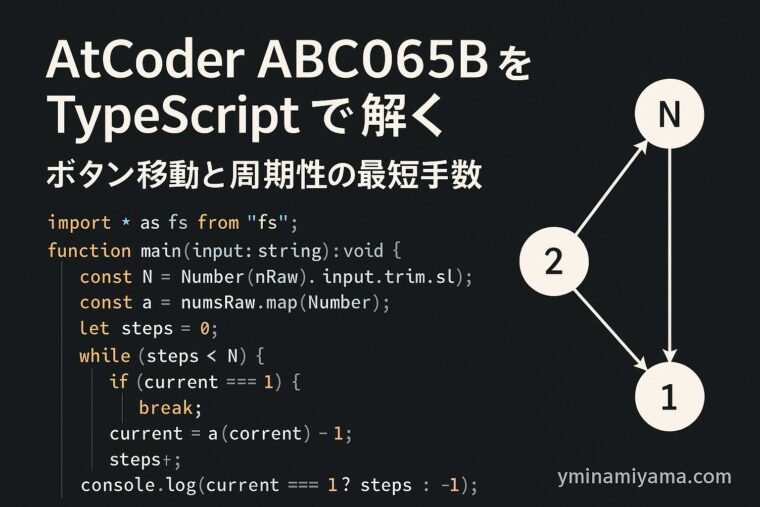
  • 各ボタンは 次に点灯するボタンが1つ に決まるので、全体は 有向グラフ（各頂点の出次数=1）＝functional graph。
  • 初期頂点 1 から、矢印に従って 1 → a1 → a[a1] → … と 一直線に辿るだけ。
  • はじめて 2 に到達した時の歩数 が答え。
  • 2 を含まない サイクル に入ったら、その後は 永遠に 2 に届かない ので -1。

初心者向けたとえ：
蛇口（現在のボタン）をひねると水（光）が次の蛇口に必ず流れる配管が1本だけ繋がっているイメージ。1番の蛇口から水を追っていき、はじめて2番に到着できるか？到着前に同じ所をぐるぐる回り始めたら、もう2番に行けない＝-1、というだけ。

ポイント

  • 最短を考える必要はありません。道は 1本 なので、「初めて到達＝最短」。
  • 訪問済み管理（visited）があると、早めに不可能判定できます（同じ頂点に再訪した瞬間に-1）。
  • 1-based の入力を 0-based に直すかどうかを最初に決めて統一。

実装例（最小・速い・わかりやすい）

import * as fs from "fs";

function main(input: string): void {
  const [nRaw, ...numsRaw] = input.trim().split(/\r?\n/);
  const N = Number(nRaw);
  const a = numsRaw.map(Number); // 1-basedの遷移先をそのまま持つ

  let steps = 0;
  let cur = 1; // 最初は1が点灯（1-basedのまま進める）

  while (steps < N && cur !== 2) { // N回たどっても着かないなら不可能
    cur = a[cur - 1]; // 0-based添字に合わせて-1
    steps++;
  }
  console.log(cur === 2 ? steps : -1);
}

const inputData = fs.readFileSync(0, "utf8");
main(inputData);

計算量：O(N) 時間、O(1) 追加メモリ

回答の良い点

  • while (count <= N) の上限で 不可能判定 はできています。
  • 1-based/0-based の変換（next = Nums[next]-1）もOK。
  • 最短性も正しく満たします（道が1本のため、初到達＝最短）。

改善のおすすめ

  • 変数名を意味で揃える（cur/steps）。
  • visited を使うと、N 未満で不可能を確定できるケースが増えて実行回数が減ることがあります。

実装例（堅牢版：訪問済みで早期終了）

import * as fs from "fs";

function main(input: string): void {
  const [nRaw, ...numsRaw] = input.trim().split(/\r?\n/);
  const N = Number(nRaw);
  const a = numsRaw.map(Number);

  const visited = new Array<boolean>(N + 1).fill(false); // 1..N をそのまま使う
  let steps = 0;
  let cur = 1;

  while (!visited[cur]) {
    if (cur === 2) {
      console.log(steps);
      return;
    }
    visited[cur] = true;
    cur = a[cur - 1];
    steps++;
  }
  console.log(-1); // サイクルに入った（2を含まないループ）
}

const inputData = fs.readFileSync(0, "utf8");
main(inputData);

計算量：O(N) 時間、O(N) メモリ（訪問管理）

サンプルで手計算

  • 例：N=3, a=[3,1,2]
    1 → 3 → 2 到達。2回で終了。
  • 不可能例：N=3, a=[1,1,1]
    1 → 1 → 1 … 2に着かないので -1。

よくある間違い

  1. オフバイワン：a[cur] としてしまい、添字ずれ。→ a[cur - 1] に統一。
  2. カウント開始位置：初期は押していないので 0。最初の遷移で +1。
  3. 初期チェック忘れ：開始時点は「1が点灯」。いきなり2ではないので、最初の1押しで2に移れるかを確認する。
  4. 無限ループ：visited 不使用で上限条件を付け忘れ。→ steps < N または visited で防止。

発展的な実装例（学習用）

  • フロイドの循環検出（Tortoise & Hare）
    2 に着く前に循環が見つかり、かつその循環が 2 を含まなければ不可能。
    ただしこの問題は道が1本なので、単純な visited の方が読みやすいことが多いです。
  • 到達回数の配列化
    「各頂点へ初めて到達するまでの手数」を配列に記録していくと、別の頂点をスタートにした派生問題に応用できます。

計算量とメモリ

  • 時間：最大で N 回の遷移
  • メモリ：最小実装は O(1)、visited を使えば O(N)

まとめ

  • 方針：1 から遷移を順に辿り、初めて 2 に到達した時の手数が答え。
  • 不可能判定：2 を含まないサイクルに入ったら -1。
  • 実装のコツ：1-based/0-based を 最初に決めて統一、上限または visited で 無限ループを防止。

RELATED POST